ENGRANAJES

Se denomina engranaje o ruedas dentadas al mecanismo utilizado para transmitir potencia de un componente a otro dentro de una máquina. Los engranajes están formados por dos ruedas dentadas, de las cuales la mayor se denomina 'corona' y la menor 'piñón'. Un engranaje sirve para transmitir movimiento circularmediante contacto de ruedas dentadas. Una de las aplicaciones más importantes de los engranajes es la transmisión del movimiento desde el eje de una fuente de energía, como puede ser un motor de combustión interna o un motor eléctrico, hasta otro eje situado a cierta distancia y que ha de realizar un trabajo. De manera que una de las ruedas está conectada por la fuente de energía y es conocido como engranaje motor y la otra está conectada al eje que debe recibir el movimiento del eje motor y que se denomina engranaje conducido.1 Si el sistema está compuesto de más de un par de ruedas dentadas, se denomina 'tren.
La principal ventaja que tienen las transmisiones por engranaje respecto de la transmisión por poleas es que no patinan como las poleas, con lo que se obtiene exactitud en la relación de transmisión.

usos de un engranaje




Ventajas del uso de engranajes
Los engranajes helicoidales pueden ser utilizados en una gran caridad de aplicaciones, ya que pueden ser montados tanto en ejes paralelos como en los que no lo son.
Presentan un comportamiento más silencioso que el de los dientes rectos usándolos entre ejes paralelos.
Poseen una mayor relación de contacto debido al efecto de traslape de los dientes.
Pueden transmitir mayores cargas a mayores velocidades debido al embonado gradual que poseen.
 Desventajas de engranajes helicoidales
La principal desventaja de utilizar este tipo de engranaje, es la fuerza axial que este produce, para contrarrestar esta reacción se tiene que colocar una chumacera que soporte axialmente y transversalmente al árbol.
clasificacion de los engranajes
La principal clasificación de los engranajes se efectúa según la disposición de sus ejes de rotación y según los tipos de dentado. Según estos criterios existen los siguientes tipos de engranajes:




Ejes paralelos
  • Cilíndricos de dientes rectos
  • Cilíndricos de dientes helicoidales
  • Doble helicoidales


Ejes perpendiculares

  • Helicoidales cruzados
  • Cónicos de dientes rectos
  • Cónicos de dientes helicoidales
  • Cónicos hipoides
  • De rueda y tornillo sin fin





Por aplicaciones especiales se pueden citar


Por la forma de transmitir el movimiento se pueden citar

  • Transmisión simple
  • Transmisión con engranaje loco
  • Transmisión compuesta. Tren de engranajes


Transmisión mediante cadena o polea dentada

  • Mecanismo piñón cadena
  • Polea dentada

 otra clasificacion 
Engranajes Helicoidales de ejes paralelos




Se emplea para transmitir movimiento o fuerzas entre ejes paralelos, pueden ser considerados como compuesto por un numero infinito de engranajes rectos de pequeño espesor escalonado, el resultado será que cada diente está inclinado a lo largo de la cara como una hélice cilíndrica.
Los engranajes helicoidales acoplados deben tener el mismo ángulo de la hélice, pero el uno en sentido contrario al otro (Un piñón derecho engrana con una rueda izquierda y viceversa). Como resultado del ángulo de la hélice existe un empuje axial además de la carga, transmitiéndose ambas fuerzas a los apoyos del engrane helicoidal.
Para una operación suave un extremo del diente debe estar adelantado a una distancia mayor del paso circular, con respecto al a otro extremo. Un traslape recomendable es 2, pero 1.1 es un mínimo razonable (relación de contacto). Como resultado tenemos que los engranajes helicoidales operan mucho más suave y silenciosamente que los engranajes rectos.
Engranajes Helicoidales de ejes cruzados


Son la forma más simple de los engranajes cuyas flechas no se interceptan teniendo una acción conjugada ( puede considerárseles como engranajes sinfín no envolventes), la acción consiste primordialmente en una acción de tornillo o de cuña, resultando un alto grado de deslizamiento en los flancos del diente.
El contacto en un punto entre diente acoplado limita la capacidad de transmisión de carga para este tipo de engranes.
Leves cambios en el ángulo de las flechas y la distancia entre centro no afectan al a acción conjugada, por lo tanto el montaje se simplifica grandemente. Estos pueden ser fabricados por cualquier máquina que fabrique engranajes helicoidales.
Engranajes helicoidales dobles







Los engranajes "espina de pescado" son una combinación de hélice derecha e izquierda. El empuje axial que absorben los apoyos o cojinetes de los engranajes helicoidales es una desventaja de ellos y ésta se elimina por la reacción del empuje igual y opuesto de una rama simétrica de un engrane helicoidal doble.
Un miembro del juego de engranes "espina de pescado" debe ser apto para absorber la carga axial de tal forma que impida las carga excesivas en el diente provocadas por la disparidad de las dos mitades del engranaje.
Un engrane de doble hélice sufre únicamente la mitad del error de deslizamiento que el de una sola hélice o del engranaje recto. Toda discusión relacionada a los engranes helicoidales sencillos (de ejes paralelos) es aplicable a loso engranajes de helicoidal doble, exceptuando que el ángulo de la hélice es generalmente mayor para los helicoidales dobles, puesto que no hay empuje axial.
características que definen un engranaje de dientes rectos









Los engranajes cilíndricos rectos son el tipo de engranaje más simple y corriente que existe. Se utilizan generalmente para velocidades pequeñas y medias; a grandes velocidades, si no son rectificados, o ha sido corregido su tallado, producen ruido cuyo nivel depende de la velocidad de giro que tengan.
  • Diente de un engranaje: son los que realizan el esfuerzo de empuje y transmiten la potencia desde los ejes motrices a los ejes conducidos. El perfil del diente, o sea la forma de sus flancos, está constituido por dos curvas evolventes de círculo, simétricas respecto al eje que pasa por el centro del mismo.
  • Módulo: el módulo de un engranaje es una característica de magnitud que se define como la relación entre la medida del diámetro primitivo expresado en milímetros y el número de dientes. En los países anglosajones se emplea otra característica llamada Diametral Pitch, que es inversamente proporcional al módulo. El valor del módulo se fija mediante cálculo de resistencia de materiales en virtud de la potencia a transmitir y en función de la relación de transmisión que se establezca. El tamaño de los dientes está normalizado. El módulo está indicado por números. Dos engranajes que engranen tienen que tener el mismo módulo.
  • Circunferencia primitiva: es la circunferencia a lo largo de la cual engranan los dientes. Con relación a la circunferencia primitiva se determinan todas las características que definen los diferentes elementos de los dientes de los engranajes.
  • Paso circular: es la longitud de la circunferencia primitiva correspondiente a un diente y un vano consecutivos.
  • Espesor del diente: es el grosor del diente en la zona de contacto, o sea, del diámetro primitivo.
  • Número de dientes: es el número de dientes que tiene el engranaje. Se simboliza como (Z). Es fundamental para calcular la relación de transmisión. El número de dientes de un engranaje no debe estar por debajo de 18 dientes cuando el ángulo de presión es 20º ni por debajo de 12 dientes cuando el ángulo de presión es de 25º.
  • Diámetro exterior: es el diámetro de la circunferencia que limita la parte exterior del engranaje.
  • Diámetro interior: es el diámetro de la circunferencia que limita el pie del diente.
  • Pie del diente: también se conoce con el nombre de dedendum. Es la parte del diente comprendida entre la circunferencia interior y la circunferencia primitiva.
  • Cabeza del diente: también se conoce con el nombre de adendum. Es la parte del diente comprendida entre el diámetro exterior y el diámetro primitivo.
  • Flanco: es la cara interior del diente, es su zona de rozamiento.
  • Altura del diente: es la suma de la altura de la cabeza (adendum) más la altura del pie (dedendum).
  • Angulo de presión: el que forma la línea de acción con la tangente a la circunferencia de paso, φ (20º ó 25º son los ángulos normalizados).
  • Largo del diente: es la longitud que tiene el diente del engranaje
  • Distancia entre centro de dos engranajes: es la distancia que hay entre los centros de las circunferencias de los engranajes.
  • Relación de transmisión: es la relación de giro que existe entre el piñón conductor y la rueda conducida. La Rt puede ser reductora de velocidad o multiplicadora de velocidad. La relación de transmisión recomendada7 tanto en caso de reducción como de multiplicación depende de la velocidad que tenga la transmisión con los datos orientativos que se indican:
Velocidad lenta: (R_t = \frac {1}{10})
Velocidad normal : (R_t = \frac {1}{7} - \frac {1}{6})
Velocidad elevada: (R_t = \frac {1}{4} - \frac {1}{2})
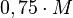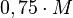Hay dos tipos de engranajes, los llamados de diente normal y los de diente corto cuya altura es más pequeña que el considerado como diente normal. En los engranajes de diente corto, la cabeza del diente vale (0,75 \cdot M), y la altura del pie del diente vale (M) siendo el valor de la altura total del diente (1,75 \cdot M)






Fórmulas constructivas de los engranajes rectos

Diámetro primitivo: D_p = Z \cdot M
Módulo: M = \frac {D_p}{Z}
Paso circular: P_c= \pi \cdot M Pc = S + W
Número de dientes: Z = \frac {D_p}{M}
Diámetro exterior: D_e = D_p + 2 \cdot M
Grueso del diente: S = \frac {P_c*19}{40}
Hueco del diente: W = \frac {P_c*21}{40}
Diámetro interior: D_i= D_p - 2,5 \cdot M
Pie del diente: 1,25 \cdot M
Cabeza del diente: M
Altura del diente: (2,25 \cdot M)
Distancia entre centros: \frac {(D_p+d_p)}{2}
Ecuación general de transmisión':  N \cdot Z= n \cdot z

Involuta del círculo base

Para el movimiento que se transmite entre un par de engranes, se suponen dos rodillos en contacto, en donde no hay deslizamiento, al diámetro de estos rodillos se les conoce como diámetro primitivo dp y al círculo que se construye con dp se le conoce como círculo primitivo. Con Un diente de engrane se pretende prolongar la acción de los rodillos, y es por esa razón que el perfil que los describe es una involuta. Para el dibujado de la involuta es necesario definir primero el círculo base (ver sig. fig.).
i.- A partir del círculo primitivo Cp, en el cuadrante superior se traza una recta horizontal tangente al círculo obteniéndose el punto A.
ii.- Luego, pasando por el punto A se traza la recta de línea de contacto de ángulo Ψ (de presión).
iii.- Seguidamente se construye el círculo base concéntrico al círculo primitivo tangente a la línea de contacto, la cual fue dibujada empleando el ángulo de presión Ψ, obteniéndose así el punto B y el radio base rb (segmento OB).


Para dibujar la involuta (ver sig. fig.) debe trazarse un radio del círculo base a un ángulo θ respecto al eje x, obteniéndose así el punto B, luego dibujamos una recta tangente a círculo base a partir del punto B y de longitud igual al arco AB, en donde A es el punto de intersección del círculo base con el eje x. obtendremos entonces un punto (x, y) que pertenece al lugar geométrico de la involuta del círculo base. Si repetimos el procedimiento anterior tres veces para distintos θ y unimos los puntos (x, y) obtenidos empleando plantillas curvas, apreciaremos un bosquejo similar al mostrado en la siguiente figura.



Las ecuaciones paramétricas que modelan el lugar geométrico de la involuta del círculo base pueden expresarse como:
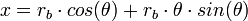
x= r_b \cdot cos(\theta) + r_b \cdot \theta \cdot sin(\theta)
y= r_b \cdot sin(\theta) - r_b \cdot \theta \cdot cos(\theta)



Suscribirse a: Entradas (Atom)